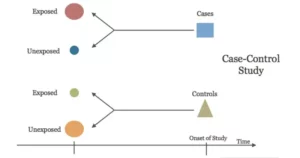
Descriptive Studies- Types, Applications, Advantages, Limitations
A simple description of the health status of a community, based on routinely available data or on data obtained in special surveys, is often the first step in an epidemiological … Read more