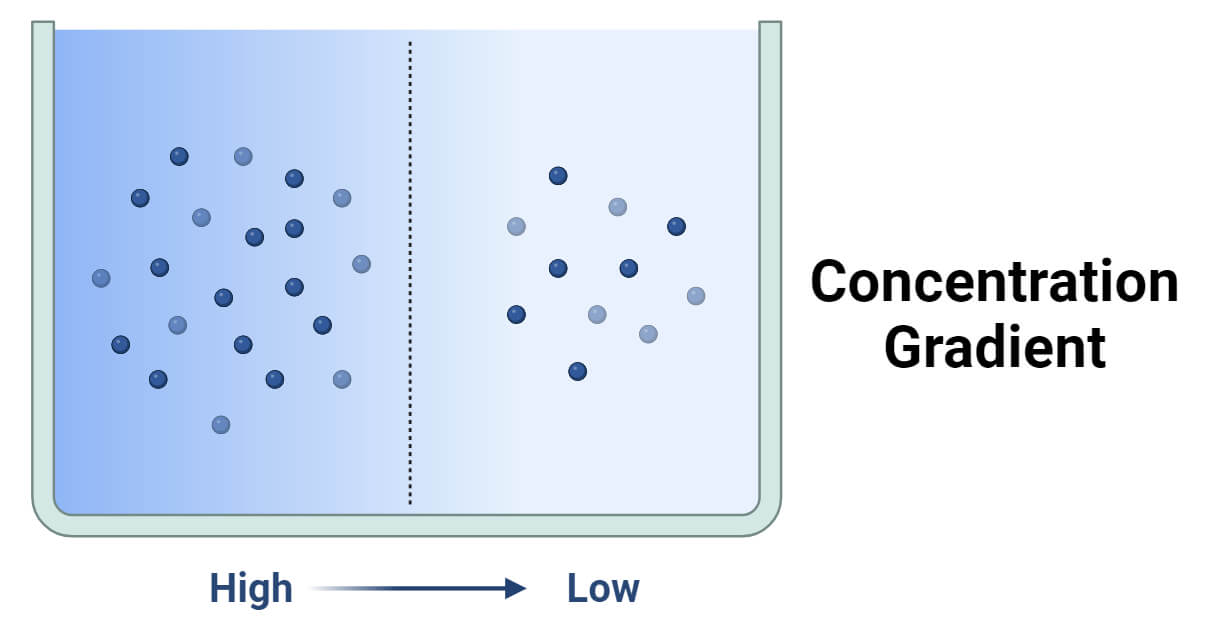
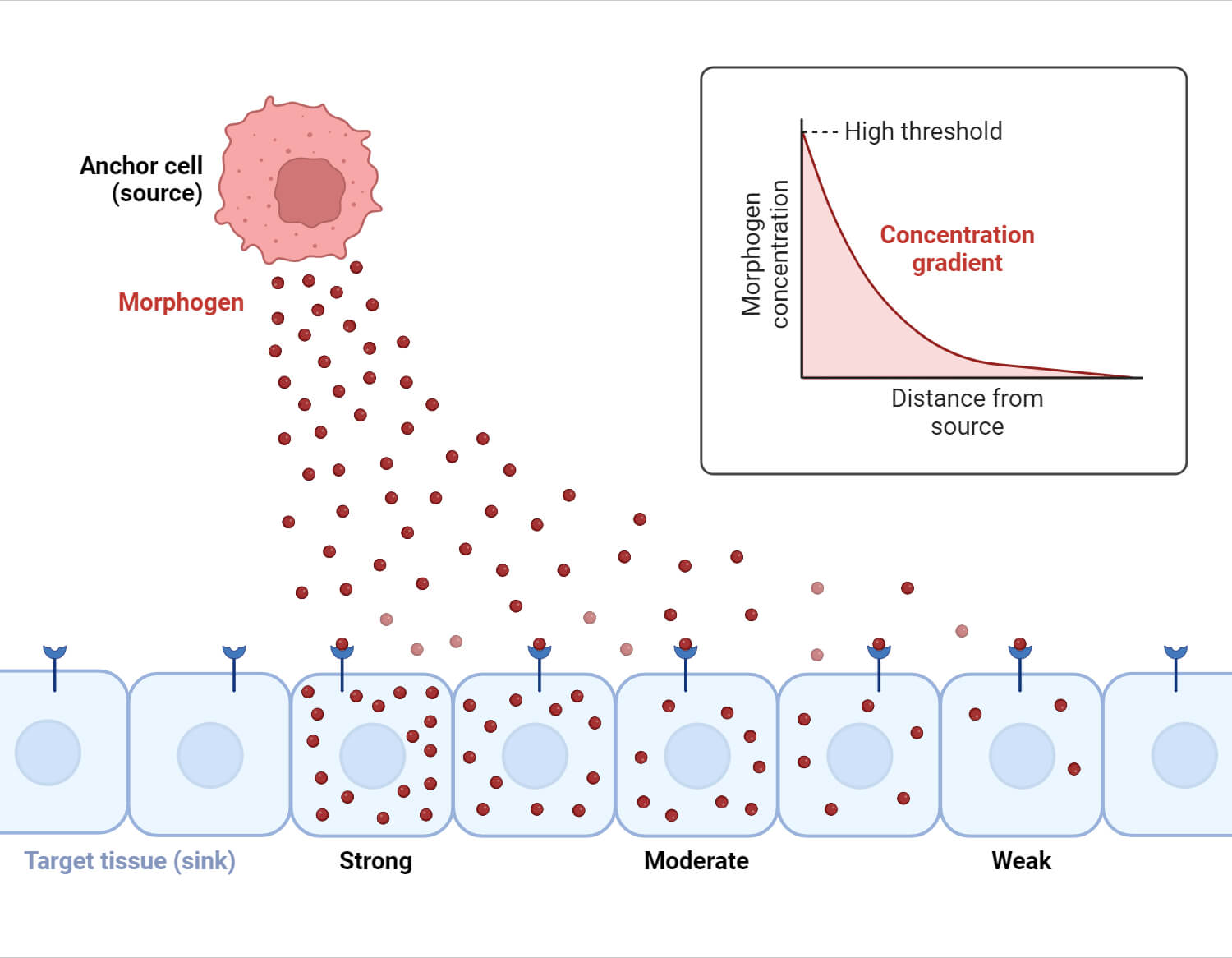
A concentration gradient refers to the gradual change in concentration of a substance within a particular region.
It represents the variation in the concentration of a solute (e.g., molecules, ions) per unit distance.
Specifically, it describes how the concentration of a substance changes over space, such as from an area of higher concentration to an area of lower concentration.
Interesting Science Videos
What is a Concentration Gradient?
The concentration gradient is a core concept in physics, chemistry, and biology. It is defined as the change in concentration of a substance over a specified distance.
It indicates how the concentration of a substance varies spatially, influencing the movement and distribution of particles.
Factors influencing concentration gradient
Temperature: Temperature affects the kinetic energy of particles, influencing their movement and diffusion. Higher temperatures generally result in a more pronounced concentration gradient due to increased molecular movement.
Permeability of the medium: The ability of a medium to allow substances to pass through affects the concentration gradient. A highly absorbent medium allows for easier diffusion and thus impacts the gradient.
Size of molecules or particles: Smaller molecules or particles can diffuse more easily, impacting the rate and extent of concentration gradient changes compared to larger ones.
Pressure differences: Pressure gradients can influence concentration gradients, especially in gases and fluids. Changes in pressure can drive the movement of molecules from regions of higher pressure to lower pressure, affecting concentration distribution.
Mathematical Representation of Concentration Gradient
Fick’s First Law
Fick’s First Law describes a substance’s diffusion rate across a concentration gradient in a homogeneous medium. The law states that the rate of diffusion (
J = − D d φ d x. Where, J: diffusion flux. D: diffusivity.
Fick’s Second Law
Fick’s Second Law extends Fick’s First Law and describes how diffusion changes the concentration profile over time. It’s a partial differential equation and is given by
dC/dt [cm-3 s-1], is proportional to the diffusivity [cm2/s] and the 2nd derivative (or curvature) of the concentration, [cm-3 cm-2] or [cm-5]
Equations Describing Concentration Gradient in Various Contexts
Chemical Reactions: Rate equations for chemical reactions often involve concentrations of reactants and products, describing how concentrations change over time during a reaction.
Types of Concentration Gradients
Linear Concentration Gradient
A linear concentration gradient refers to a steady, uniform increase or decrease in concentration over a defined distance. The change in concentration is proportional to the distance.
Non-linear Concentration Gradient
A non-linear concentration gradient refers to an uneven or irregular change in concentration over a defined distance. The rate of change in concentration is not constant.
Steep Concentration Gradient
A steep concentration gradient indicates a rapid and significant change in concentration over a short distance. This gradient is often observed when there’s a sharp transition between regions with different concentrations.
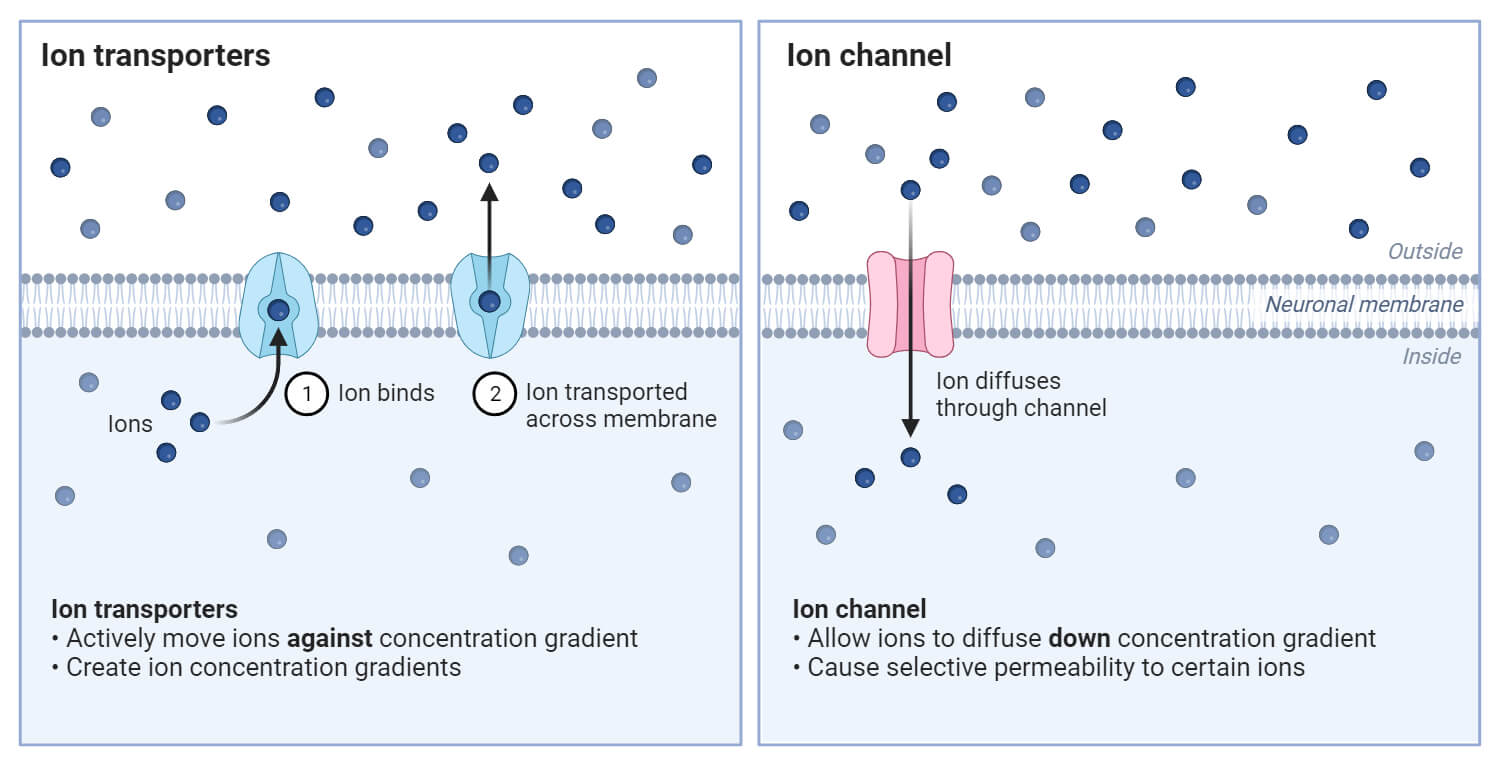
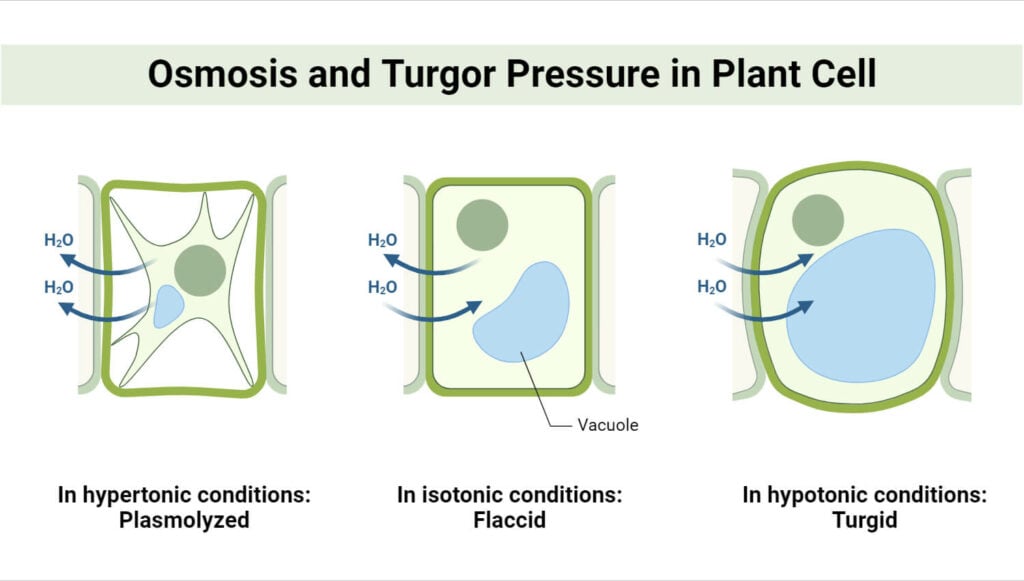
Biological Applications of Concentration Gradient
Cellular Processes
- Diffusion: Movement of molecules from an area of high concentration to an area of low concentration.
- Osmosis: Water movement across a semi-permeable membrane from a dilute solution to a more concentrated one.
- Active Transport: Energy-dependent movement of molecules against their concentration gradient.
Role in Physiological Functions
- Nervous System Signaling: Ion concentration gradients are crucial in generating electrical signals in neurons.
- Respiratory and Circulatory Systems: Oxygen and carbon dioxide move across concentration gradients during respiration and circulation.
Chemical Applications of Concentration Gradient
The concentration gradient plays a crucial role in chemical reactions by influencing the reactants’ transformation rate into products.
According to the principles outlined in Fick’s laws, a higher concentration gradient between reactants increases the diffusion rate.
It leads to more frequent collisions between particles. The increased collision frequency enhances the likelihood of successful reactions and accelerates the reaction rate. In simple terms, a steeper concentration gradient drives reactions to proceed more rapidly.
Concentration gradients and Industrial Processes
Concentration gradients are utilized in various separation techniques crucial to industrial processes. Distillation, for example, exploits the concentration gradient of different components in a mixture based on their varying boiling points.
The more volatile component with a higher concentration evaporates more readily, creating a concentration gradient in the vapor phase that aids separation.
Similarly, chromatography employs the principle of differential partitioning of components between a stationary phase and a mobile phase.
The concentration gradient between the stationary and mobile phases helps separate and analyze mixtures based on differences in molecular interactions, affinities, or sizes of the components.
Environmental Applications of Concentration Gradient
Concentration gradients are fundamental in understanding the dispersion and movement of environmental pollutants. When pollutants are released into the environment, their concentration gradients dictate their spread and movement.
The concentration gradient influences the direction and extent of pollutant dispersal, affecting the environmental impact and potential risks to ecosystems and human health.
Monitoring and assessing environmental conditions often involve analyzing concentration gradients of specific substances.
For instance, measuring the concentration gradients of pollutants like particulate matter, gases, or volatile organic compounds in air quality monitoring allows for assessing pollution levels.
Conclusion
Concentration gradients are pivotal in shaping chemical reactions, influencing reaction rates, and facilitating industrial separation processes.
Additionally, they are essential for understanding environmental pollutant dispersion and enabling effective monitoring for a sustainable and healthier environment.
Harnessing the power of concentration gradients is fundamental for advancements across scientific and environmental domains.
References
- https://www.mit.edu/~kardar/teaching/projects/chemotaxis(AndreaSchmidt)/gradients.htm
- https://www.sciencedirect.com/topics/engineering/concentration-gradient
- https://www.nottingham.ac.uk/nmp/sonet/rlos/science/osmosis/page5.html
- https://askabiologist.asu.edu/concentration-gradients
- https://www.bbc.co.uk/bitesize/guides/zsgfv4j/revision/4
- https://pubs.rsc.org/en/content/articlelanding/2017/ra/c7ra04494a
- https://www.sciencefacts.net/concentration-gradient.html
