
Image Source: AB Tasty.
Interesting Science Videos
Type 1 error definition
- Type 1 error, in statistical hypothesis testing, is the error caused by rejecting a null hypothesis when it is true.
- Type 1 error is caused when the hypothesis that should have been accepted is rejected.
- Type I error is denoted by α (alpha), known as an error, also called the level of significance of the test.
- This type of error is a false positive error where the null hypothesis is rejected based on some error during the testing.
- The null hypothesis is set to state that there is no relationship between two variables and the cause-effect relationship between two variables, if present, is caused by chance.
- Type 1 error occurs when the null hypothesis is rejected even when there is no relationship between the variables.
- As a result of this error, the researcher might believe that the hypothesis works even when it doesn’t.
Type 1 error causes
- Type 1 error is caused when something other than the variable affects the other variable, which results in an outcome that supports the rejection of the null hypothesis.
- Under such conditions, the outcome appears to have happened due to some causes than chance when it is caused by chance.
- Before a hypothesis is tested, a probability is set as a level of significance which means that the hypothesis is being tested while taking a chance where the null hypothesis is rejected even when it is true.
- Thus, type 1 error might be due to the chance/ level of significance set before the test without considering the test duration and sample size.
Probability of type 1 error
- The probability of Type I error is usually determined in advance and is understood as the significance level of testing the hypothesis.
- If the Type I error is fixed at 5 percent, there are about five chances in 100 that the null hypothesis, H0, will be rejected when it is true.
- The rate or probability of type 1 error is symbolized by α and is also termed the level os significance in a test.
- It is possible to reduce type 1 error at a fixed size of the sample; however, while doing so, the probability of type II error increases.
- There is a trade-off between the two errors where decreasing the probability of one error increases the probability of another. It is not possible to reduce both errors simultaneously.
- Thus, depending on the type and nature of the test, the researchers need to decide the appropriate level of type 1 error after evaluating the consequences of the errors.
Type 1 error examples
- For this, let us take a hypothesis where a player is trying to find the relationship between him wearing new shoes and the number of wins for his team.
- Here, if the number of wins for his team is more when he was wearing his new shoes is more than the number of wins for his team otherwise, he might accept the alternative hypothesis and determine that there is a relationship.
- However, the winning of his team might be influenced by just chance rather than his shoes which results in a type 1 error.
- In this case, he should’ve accepted the null hypothesis because the winning of a team might happen due to chance or luck.
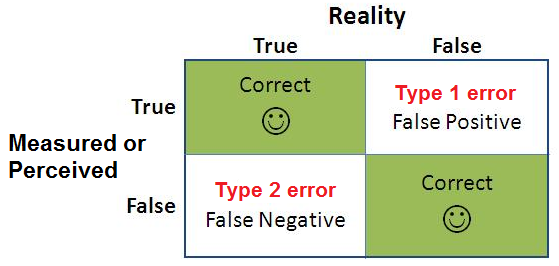
Image Source: AB Tasty.
Type II error definition
- Type II error is the error that occurs when the null hypothesis is accepted when it is not true.
- In simple words, Type II error means accepting the hypothesis when it should not have been accepted.
- The type II error results in a false negative result.
- In other words, type II is the error of failing to accept an alternative hypothesis when the researcher doesn’t have adequate power.
- The Type II error is denoted by β (beta) and is also termed the beta error.
- The null hypothesis states that there is no relationship between two variables, and the cause-effect relationship between two variables, if present, is caused by chance.
- Type II error occurs when the null hypothesis is acceptable considering that the relationship between the variables is because of chance or luck, and even when there is a relationship between the variables.
- As a result of this error, the researcher might believe that the hypothesis doesn’t work even when it should.
Type II error causes
- The primary cause of type II error, like a Type II error, is the low power of the statistical test.
- This occurs when the statistical is not powerful and thus results in a Type II error.
- Other factors, like the sample size, might also affect the test results.
- When small sample size is selected, the relationship between the two variables being tested might not be significant even when it does exist.
- The researcher might assume the relationship is due to chance and thus reject the alternative hypothesis even when it is true.
- There it is important to select an appropriate size of the sample before beginning the test.
Probability of type II error
- The probability of committing a Type II error is calculated by subtracting the power of the test from 1.
- If Type II error is fixed at 2 percent, there are about two chances in 100 that the null hypothesis, H0, will be accepted when it is not true.
- The rate or probability of type II error is symbolized by β and is also termed the error of the second type.
- It is possible to reduce the probability of Type II error by increasing the significance level.
- In this case, the probability of rejecting the null hypothesis even when it is true also increases, decreasing the chances of accepting the null hypothesis when it is not true.
- However, because type I and Type II error are interconnected, reducing one tends to increase the probability of the other.
- Therefore, depending on the nature of the test, it is important to determine which one of the errors is less detrimental to the test.
- For this, if a type I error involves the time and effort of retesting the chemicals used in medicine, that should have been accepted. In contrast, the type II error involves the chances of several users of this medicine being poisoned, and it is wise to accept the type I error over type II.
Type II error examples
- For this, let us take a hypothesis where a shepherd thinks there is no wolf in the village, and he wakes up all night for five nights to determine the wolf’s existence.
- If he sees no wolf for five nights, he might assume that there is no wolf in the village where the wolf might exist and attack the sixth night.
- In this case, when the shepherd accepts that no wolf exists, a type II error results where he agrees with the null hypothesis even when it is not true.
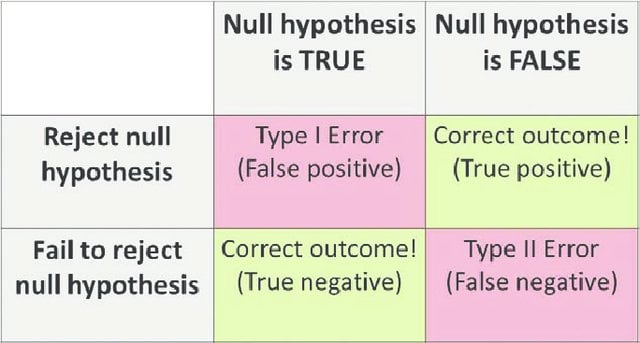
Type I Error vs. Type II Error
| Basis for comparison | Type I Error | Type II Error |
| Definition | Type 1 error, in statistical hypothesis testing, is the error caused by rejecting a null hypothesis when it is true. | Type II error is the error that occurs when the null hypothesis is accepted when it is not true. |
| Also termed | Type I error is equivalent to a false positive. | Type II error is equivalent to a false negative. |
| Meaning | It is a false rejection of a true hypothesis. | It is the false acceptance of an incorrect hypothesis. |
| Symbol | Type I error is denoted by α. | Type II error is denoted by β. |
| Probability | The probability of type I error is equal to the level of significance. | The probability of type II error is equal to one minus the power of the test. |
| Reduced | It can be reduced by decreasing the level of significance. | It can be reduced by increasing the level of significance. |
| Cause | It is caused by luck or chance. | It is caused by smaller sample size or a less powerful test. |
| What is it? | Type I error is similar to a false hit. | Type II error is similar to a miss. |
| Hypothesis | Type I error is associated with rejecting the null hypothesis. | Type II error is associated with rejecting the alternative hypothesis. |
| When does it happen? | It happens when the acceptance levels are set too lenient. | It happens when the acceptance levels are set too stringent. |
Type I Error vs. Type II Error Video
References and Sources
- R. Kothari (1990) Research Methodology. Vishwa Prakasan. India.
- https://magoosh.com/statistics/type-i-error-definition-and-examples/
- https://corporatefinanceinstitute.com/resources/knowledge/other/type-ii-error/
- https://keydifferences.com/difference-between-type-i-and-type-ii-errors.html
- 3% – https://www.investopedia.com/terms/t/type-ii-error.asp
- 1% – https://www.thoughtco.com/null-hypothesis-examples-609097
- 1% – https://www.thoughtco.com/hypothesis-test-example-3126384
- 1% – https://www.stt.msu.edu/~lepage/STT200_Sp10/3-1-10key.pdf
- 1% – https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2996198/
- 1% – https://www.chegg.com/homework-help/questions-and-answers/following-table-shows-number-wins-eight-teams-football-season-also-shown-average-points-te-q13303251
- 1% – https://stattrek.com/hypothesis-test/power-of-test.aspx
- 1% – https://statisticsbyjim.com/hypothesis-testing/failing-reject-null-hypothesis/
- 1% – https://simplyeducate.me/2014/05/29/what-is-a-statistically-significant-relationship-between-two-variables/
- 1% – https://abrarrazakhan.files.wordpress.com/2014/04/mcq-testing-of-hypothesis-with-correct-answers.pdf
- <1% – https://www.nature.com/articles/s41524-017-0047-6
- <1% – https://www.dummies.com/education/math/statistics/understanding-type-i-and-type-ii-errors/
- <1% – https://www.chegg.com/homework-help/questions-and-answers/null-hypothesis-true-possibility-making-type-error-true-false-believe-s-false-want-make-su-q4115439
- <1% – https://stepupanalytics.com/hypothesis-testing-examples/
- <1% – https://statistics.laerd.com/statistical-guides/hypothesis-testing-3.php
- <1% – https://mpra.ub.uni-muenchen.de/66373/1/MPRA_paper_66373.pdf
- <1% – https://en.wikipedia.org/wiki/Probability_of_error
- <1% – https://educationalresearchtechniques.com/2016/02/03/type-i-and-type-ii-error/

