Interesting Science Videos
Transposable elements definition
Transposable elements (TE) or transposons can be defined as small, mobile DNA sequences that move around chromosomes with no regard for homology, and insertion of these elements may produce deletions, inversions, chromosomal fusions, and even more complicated rearrangements.
- Transposons are mobile genetic elements that often carry an antimicrobial resistance gene.
- These elements can insert randomly, move from plasmids to the chromosome, and vice versa, and can be moved from one bacterium to another by conjugation, transformation, or transduction.
- Transposable elements make up a significant fraction of the genome and are responsible for much of the mass of DNA in a eukaryotic cell.
- Transposable elements were discovered by Barbara McClintock (1965) through an analysis of genetic instability in maize (corn).
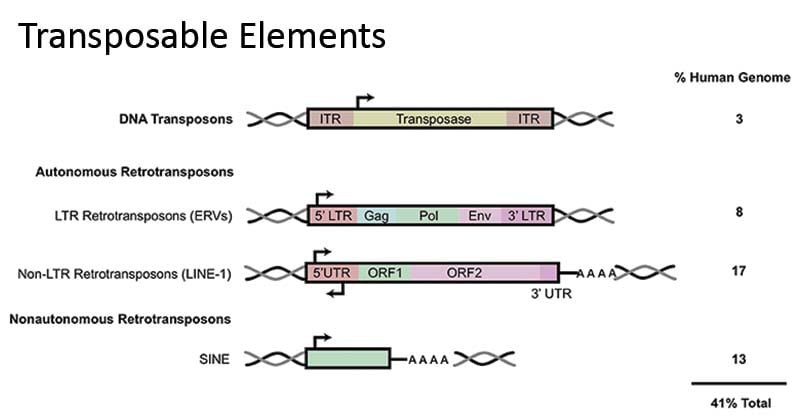
Figure: Transposable elements in the human genome. Image Source: https://doi.org/10.3389/fneur.2019.00894
Characteristics of transposable elements
Some salient features of transposable elements are:
- These are the DNA sequences that code for enzymes which result in self-duplication and insertion into a new DNA site.
- Transposons are involved in transposition events which include both recombination and replication, which usually generates two copies of the original transposable elements. One of the copies remains at the parent site, whereas the other one reaches the target site on the host chromosome.
- The integrity of the target genes of these elements is invariably disrupted by the presence of those elements.
- Because transposons carry the genes for initiation of RNA synthesis, some previously dormant genes might be activated.
- A transposable element doesn’t have a site for the origin of replication. As a result, it cannot replicate without the host chromosome as plasmids or phages.
- There is no homology between the transposon and its target site for insertion. These elements can insert at almost any position in the host chromosome or a plasmid. Some transposons might seem likely to enter at some specific positions (hot spots), they barely insert at base-specific target sites.
Types of Transposable elements
Transposable elements are of the following two types:
Insertion Sequences (IS) or Simple Transposons
- The insertion sequences (IS) or simple transposons are shorter sequences (800 to 1500 bp) and do not code for proteins.
- These sequences carry the genetic information necessary for their transposition (e., the gene for the enzyme transposase)
- Insertion sequences have been identified in bacteriophages, in F factor plasmid and many bacteria.
Transposons (Tn) or Complex Transposons
- Transposons (Tn) or complex transposons are several thousand base pair long, and have genes that code for one or more proteins which might include resistance factors in bacteria acting against antibiotics.
- A distinguishing character of a transposon is the presence of identical, inverted terminal repeat (IR) sequences ranging from 8 to 38 base pairs (b.p.)
- These inverted repeats are unique to different types of transposons.
- A short (less than ten b.p.) sequence is present on either side of a transposon.
- The insertion of transposon causes duplication of a singular target sequence, which then appear as direct repeats flanking the inserted transposable element.
- The flanking direct repeats are not considered part of the transposon. These repeat sequences themselves act like IS or IS-like segments.
Examples of Transposable elements
Tn 3 transposon of E. coli
- Tn 3 transposon has 4957 bp and contains three genes such as tnp A, tnp R and
- Tnp A codes for transposase having 1015 amino acids and required for transposition.
- Tnp R codes for a repressor (also called resolvase), containing 185 amino acids, which regulates the transposase.
- Bla codes for a β-lactamase enzyme which confers resistance to the antibiotic ampicillin.
Bacteriophage Mu
- The bacteriophage Mu (Mu = mutator) is a temperate bacteriophage having usual phage properties and could be regarded as a large transposon.
- It inserts itself into the coli chromosome at random locations resulting in a mutation.
Yeast Ty elements
- These elements are found in yeast Saccharomyces cerevisiae which are about 5900 base pairs long
- Ty elements are surrounded by five base-pair direct repeats which are created by the duplication of DNA present at the site of the Ty
Applications of transposable elements
- Transposable elements can be used as a genetic tool for the analysis of gene expression and protein functioning.
- These are used in genetic engineering to insert or remove specific genetic sequences, and also to cause frameshift mutation.
- The Tc1/mariner-class of TEs Sleeping Beauty transposon system is being studied for use in human gene therapy.
Negative effects of transposable elements
- A transposable gene, when inserted into a functional gene, might disable the gene.
- Multiple copies of the same sequence hinder the chromosome pairing during cell division resulting in chromosome duplication.
- Expression of harmful disease-causing proteins in the transposons affects the normal cellular function.
References
- Verma PS and Agarwal VK (2005). Cell Biology, Genetics, Molecular Biology, Evolution, and Ecology. Multicolored Edition.
- McGee, David & Coker, Christopher & Harro, Janette & Mobley, Harry. (2001). Bacterial Genetic Exchange. Doi: 10.1038/npg.els.0001416.
Internet Sources
- 7% – http://www.yourarticlelibrary.com/biology/brief-notes-on-simple-transposons-complex-transposons-discussed/3852
- 3% – https://www.svpgcollege.org.in/transposable-genetic-elements-jumping-genes/
- 3% – https://studydocz.com/brief-notes-on-simple-transposons-complex-transposons-discussed-28119
- 2% – https://wiki2.org/en/Transposable_element
- 2% – https://en.wikipedia.org/wiki/Transposable_elements
- 1% – https://resources.saylor.org/wwwresources/archived/site/wp-content/uploads/2012/02/BIO401_Wikipedia_Transposable-elements_2.7.2012.pdf
- 1% – https://quizlet.com/60469835/transposable-elements-flash-cards/
- 1% – https://en.wikipedia.org/wiki/Episome
- 1% – http://www.yourarticlelibrary.com/biology/6-most-important-characteristics-of-transposable-elements-biology/6348
- 1% – http://www.bx.psu.edu/~ross/workmg/TranspositionCh9.pdf
- <1% – https://www.sciencedirect.com/science/article/pii/B978012301463450005X
- <1% – https://academic.oup.com/hmg/article/20/R1/R14/632060
