Plastids- Definition, Structure, Types, Functions and Diagram

Plastids Definition

• Plastid is a double membrane-bound organelle involved in the synthesis and storage of food, commonly found within the cells of photosynthetic plants.
• Plastids were discovered and named by Ernst Haeckel, but A. F. W. Schimper was the first to provide a clear definition.
• They are necessary for essential life processes, like photosynthesis and food storage. 
• A plastid containing green pigment (chlorophyll) is called chloroplast whereas a plastid containing pigments apart from green is called a chromoplast. A plastid that lacks pigments is called a leucoplast and is involved mainly in food storage.

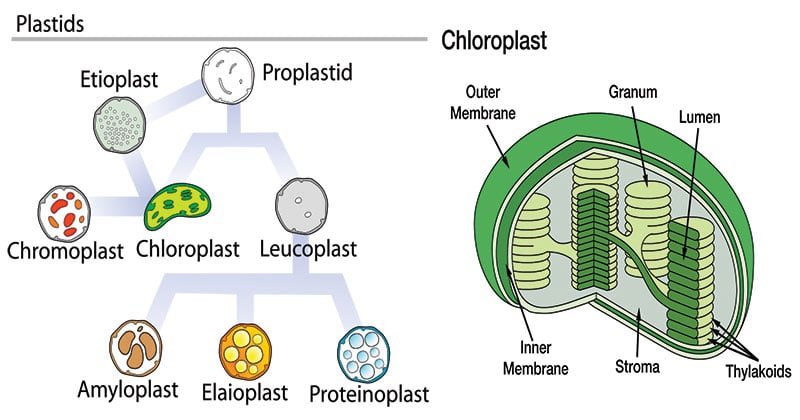
Figure: Diagram of Plastids

Types of Plastids

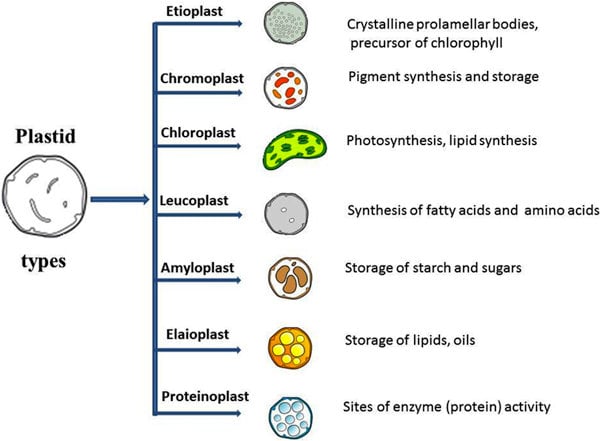
Image Source: Sitanshu Sekhar Sahu (https://doi.org/10.1186/1471-2105-14-S14-S7)

An undifferentiated plastid is called a proplastid. It may develop later into any of the other plastids.

A. Chloroplasts

• The chloroplasts are probably the most-known of the plastids.
• These are responsible for photosynthesis.
• The chloroplast is filled with thylakoids, which is where photosynthesis occurs, and chlorophyll remains.

B. Chromoplasts

• Chromoplasts are units where pigments are stored and synthesized in the plant.
• These are found in flowering plants, fruits, and aging leaves.
• The chloroplasts actually convert over to chromoplasts.
• The carotenoid pigments allow for the different colors seen in fruits and the fall leaves. One of the main reasons for these structures and the colors is to attract pollinators.

C. Leucoplasts

• Leucoplasts are the non-pigmented organelles.
• They are found in the non-photosynthetic parts of the plant, such as the roots.
• Depending on what the plant needs, they may become essentially just storage sheds for starches, lipids, and proteins.
• They are more readily used for synthesizing amino acids and fatty acids.
• A leucoplast may be an amyloplast that stores starch, an elaioplast that stores fat, or a proteinoplast that stores proteins.

D. Gerontoplasts 

• Gerontoplasts are basically chloroplasts that are going through the aging process.
• These are chloroplasts of the leaves that are beginning to convert into different organelles or are being re-purposed since the leaf is no longer utilizing photosynthesis (such as in the fall months).

Depending on their morphology and function, plastids have the ability to differentiate or redifferentiate, between these and other forms.

Structure of Plastids

• Chloroplasts may be spherical, ovoid, or discoid in higher plants and stellate, cup-shaped, or spiral as in some algae.
• They are usu­ally 4-6 µm in diameter and 20 to 40 in number in each cell of higher plants, evenly distributed throughout the cytoplasm.
• The chloroplast is bounded by two lipoprotein membranes, an outer and an inner membrane, with an intermembrane space between them.
• The inner membrane encloses a matrix, the stroma which contains small cylindri­cal structures called grana. Most chloroplasts con­tain 10-100 grana.

The Grana and Thylakoids

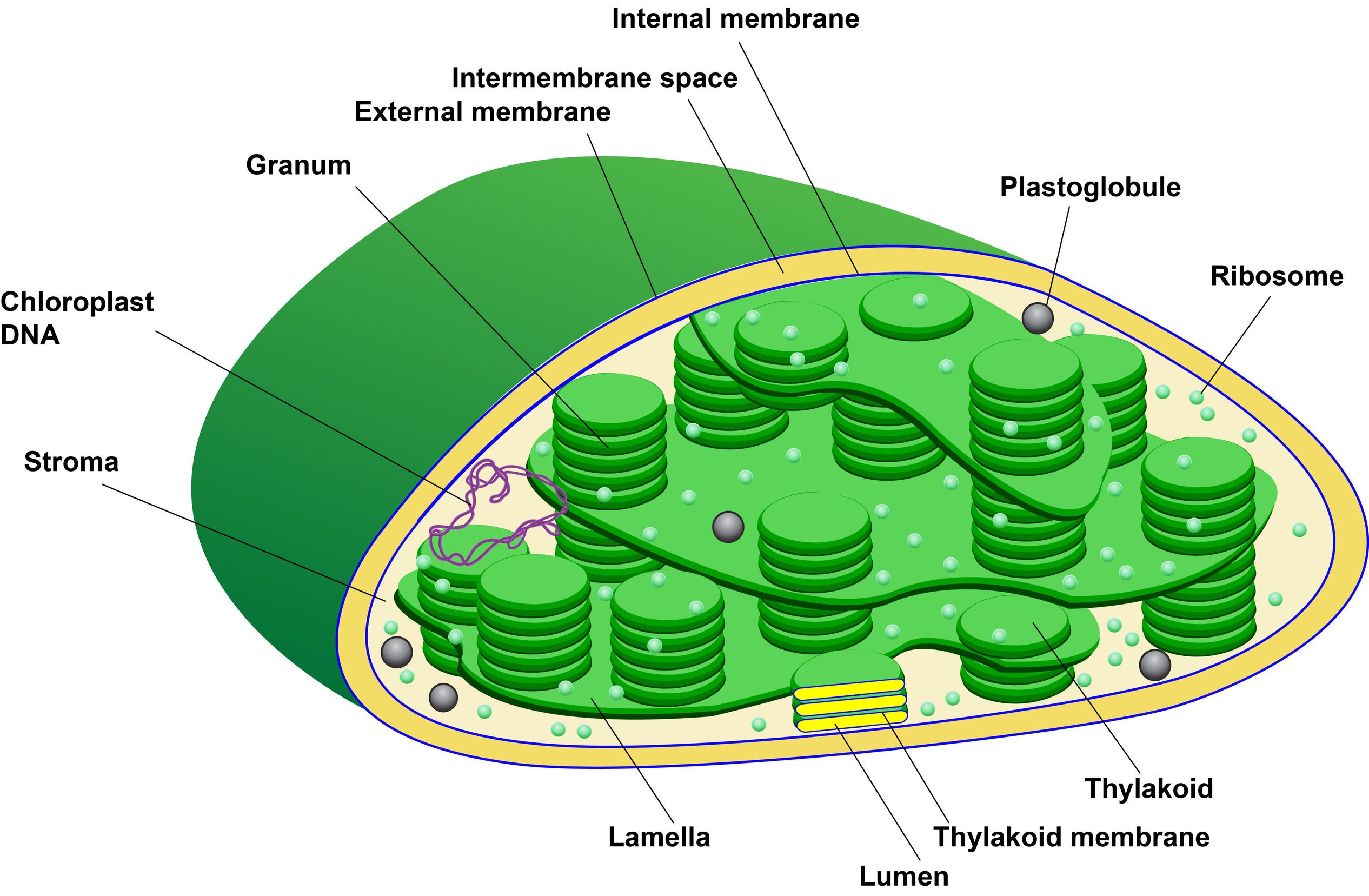
Image Credit: Luiz Fernando Botter.

• Each granum has a number of disc-shaped membranous sacs called grana lamellae or thylakoids (80-120Å across) piled one over the other.
• The grana are intercon­nected by a network of anastomosing tubules called inter-grana or stroma lamellae.
• Single thylakoids, called stroma thylakoids, are also found in chloroplasts.
• Electron dense bodies, osmophilic granules along with ribosomes (70S), circular DNA, RNA and soluble enzymes of Calvin cycles are also present in the matrix of the stroma.
• Chloroplasts thus have three different mem­branes, the outer, the inner and the thylakoid membrane.
• The thylakoid membrane consists of lipoprotein with a greater amount of lipids which are galactolipids, sulpholipids, phospholipids.
• The inner surface of the thylakoid membrane is gra­nular in the organization due to small spheroidal quantosomes.
• The quantosomes are the photosynthetic units, and consist of two structurally distinct photosystems, PS I and PS II, containing about 250 chlorophyll molecules. Each photosystem has antenna chlorophyll com­plexes and one reaction center in which energy conversion takes place. In higher plants, the pig­ments present are chlorophyll-a, chlorophyll-b, carotene, and xanthophyll.
• The two photosystems and the components of the electron transport chain are asymmetrically distributed across the thylakoid membrane. Electron acceptors of both PS I and PS II are on the outer (stroma) surface of the thylakoid membrane. Electron donors of PS I are on the inner (thylakoid space) surface.

Functions

All plant cells contain plastids in some shape or form. This roll-call indicates their functional diversity and demonstrates that plastids lie at the very core of plant cellular function. 

• Plastids are the site of manufacture and storage of important chemical compounds used by the cells of autotrophic eukaryotes.
• The thylakoid membrane contains all the enzymatic components required for photosyn­thesis. Interaction between chlorophyll, electron carriers, coupling factors, and other components takes place within the thylakoid membrane. Thus the thylakoid membrane is a specialized struc­ture that plays a key role in the capture of light and electron transport.
• Thus, chloroplasts are the centers of synthesis and metabolism of carbohydrates.
• They are not only of crucial importance in photosynthesis but also in the storage of primary foodstuffs, particularly starch.
• Its function largely depends on the presence of pigments. A plastid involved in food synthesis typically contains pigments, which are also the ones responsible for the color of a plant structure (e.g. green leaf, red flower, yellow fruit, etc.).
• Like mitochondria, plastids have their own DNA and ribosomes. Hence, they may be used in phylogenetic studies.

References

1. Smith, C. M., Marks, A. D., Lieberman, M. A., Marks, D. B., & Marks, D. B. (2005). Marks’ basic medical biochemistry: A clinical approach. Philadelphia: Lippincott Williams & Wilkins.
2. http://www.biologydiscussion.com/plastids/plastids-types-structure-and-function-with-diagram/38591
3. Koolman, J., & Röhm, K.-H. (2005). Color atlas of biochemistry. Stuttgart: Thieme.
4. Alberts, B. (2004). Essential cell biology. New York, NY: Garland Science Pub.
5. Verma, P. S., & Agrawal, V. K. (2006). Cell Biology, Genetics, Molecular Biology, Evolution & Ecology (1 ed.). S .Chand and company Ltd.
6. https://www.biology-online.org/dictionary/Plastid
7. https://study.com/academy/lesson/plastids-definition-structure-types-functions.html
8. Leegood R. C. (2010). Plastid biology. Annals of Botany, 106(1), ix.
9. https://www.britannica.com/science/plastid