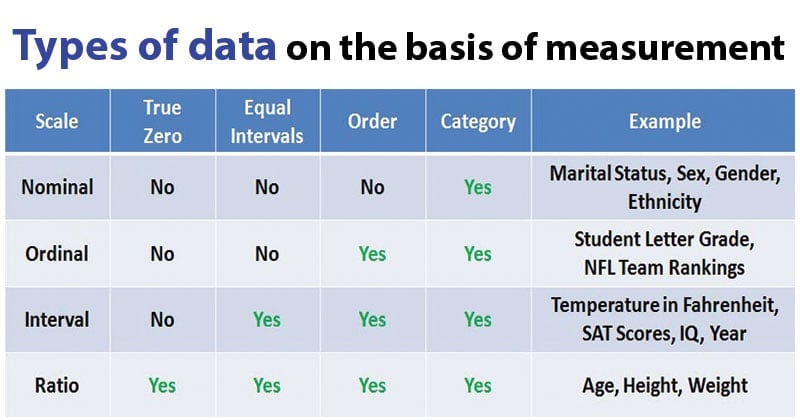
- Depending on the measurements, there are four different types of data that can be achieved.
- These different types of data are nominal, ordinal, interval and ratio data.
- These different variances of data vary in complexity of obtaining.
Interesting Science Videos
Nominal Data
- Nominal data is the least complex of the four types of data.
- Nominal or categorical data is data that comprises of categories that cannot be rank ordered – each category is just different.
- The categories available cannot be placed in any order and no judgment can be made about the relative size or distance from one category to another. This is to say no mathematical operations can be performed on the data relative to each other.
- It consists of absolute codes or names that are used mainly for tallying at the end.
- One would use nominal data to keep mutual exclusiveness between subjects.
- For example, when conducting a study the experimenter may decide to apply the symbols M & F to represent male and female participants. At the end of the study, these symbols are then tallied to determine how many males and females participants there were, nothing more.
- Another example is in grammar, the many parts of speech: noun, verb, preposition, article, pronoun, etc. These different parts/codes make up sentences that makeup paragraphs, which produce stories that become speeches, books, articles, etc.
Ordinal Data
- Ordinal Data consist of the natural order, hence the name: ordinal.
- Ordinal operates off rankings or ratings, but the distances between differences do not have a relative degree.
- It is the data that comprises of categories that can be rank ordered.
- Like with the nominal data the distance between each category cannot be calculated but the categories can be ranked above or below each other.
- Only statistical judgments and limited maths can be performed.
- For example, on a scale a participant is directed to rank their satisfaction level between 1 and 10, although a ranking of 7 is one step above a ranking of 6 this does not necessarily mean that the difference between a ranking of 9 and a ranking of 10 are the same as the difference between a ranking of 7 and a ranking of 6.
- One more example includes a race or some type of competition where a ranking system is in place, there will be a 1st place winner, 2nd place winner, 3rd place winner, and so on. These rankings only show the order of completion or a spot on an ordered plane.
Interval Data
- In ordinal scales, the interval between adjacent values is not constant. For example, the difference in finishing time between the 1st place horse and the 2nd horse need not the same as that between the 2nd and 3rd place horses.
- An interval scale has a constant interval but lacks a true 0 point. As a result, one can add and subtract values on an interval scale, but one cannot multiply or divide units.
- Hence, it is similar to ordinal but the differences or intervals between values or rankings are equally split. Therefore, the difference between a ranking of a 7 and a 6 is the same as the difference between a ranking of a 9 and a 10 on a 10-point scale.
- One real-world example of interval data is a 12-hour analog clock that measures the time of day. The clock has equal intervals; the time it takes for the big hand to go from the 1 to the 2 is the same as the time it takes to go from the 9 to the 10.
Ratio Data
- Ratio data is the most complex of the fours scales of measurement, as well as the most preferred scale of measurement.
- It has all the same properties of interval data but possesses a natural zero, meaning there is a point where that measurement, whatever it may be, is not existing.
- A ratio scale has the property of equal intervals but also has a true 0 point. As a result, one can multiply and divide as well as add and subtract using ratio scales.
- Variables such as height weight and duration are ratio data.
- All these variables can have a value of zero that represents nothing being there nullity.
- A real-world example of ratio data is income: money earned in a time period. One can either earn $0 in a month or any other dollar amount higher than zero.
References
- Kumar, Ranjit. Research Methodology: A Step-by-Step Guide for Beginners. Los Angeles: SAGE, 2011. Print.
- https://www.cise.ufl.edu/class/cis6930sp15res/week3_lecture2_scribe1.pdf
- http://athena.ecs.csus.edu/~buckley/CSc238/Types%20of%20Data.pdf
- https://www.albany.edu/~msz03/sta552/pennstate/types_of_data.pdf
- https://is.muni.cz/el/1456/podzim2015/MPH_CSMR/um/51765602/2_Types_of_Data.pdf
- http://homepage.stat.uiowa.edu/~rdecook/stat1010/notes/Section_2.1_2.2_data_types_and_errors.pdf
- http://www.stat.purdue.edu/~huang251/slides25.pdf
- http://psych.colorado.edu/~carey/courses/psyc5741/handouts/Measurement%20Scales.pdf
