The Beer-Lambert law, also known as Beer’s law, the Lambert-Beer law, or the Beer-Lambert–Bouguer law relates the attenuation of light to the properties of the material through which the light is traveling.
What is Beer-Lambert Law?
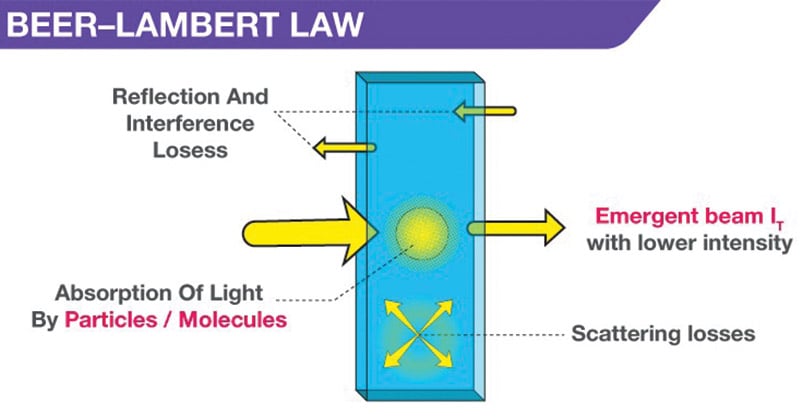
- When a monochromatic light of initial intensity Io passes through a solution in a transparent vessel, some of the light is absorbed so that the intensity of the transmitted light I is less than Io.
- There is some loss of light intensity from scattering by particles in the solution and reflection at the interfaces, but mainly from absorption by the solution.
- The relationship between I and Io depends on the path length of the absorbing medium, l, and the concentration of the absorbing solution, c. These factors are related in the laws of Lambert and Beer.
Derivation of Beer-Lambert Law
- If material bodies are exposed to radiation, part of the incident radiation is absorbed, a part is scattered and a part is transmitted.
- As a result of absorption the intensity of light passing through material bodies, i.e. the intensity of transmitted light, decreases.
- The fraction of incident light absorbed depends on the thickness of the absorbing medium.
- Lambert derived a quantitative relationship between the decrease in intensity of a monochromatic light due to the passage through a homogeneous medium of thickness dx and the intensity of light I. This law is known as Lamberts law, and may be stated as
- The decrease in intensity of light with thickness of the absorbing medium at any point is directly proportional to the intensity of light.
Mathematically it can be expressed as
– ???????? / ???????? ∝ ???? — — — — — — (1)
Where dI is a small decrease in intensity of light upon passing through a small distance dx and I is the intensity of the monochromatic light just before entering the medium.
Equation (1) may be written as
– ???????? / ???????? = ???????? — — — — — — (2)
Where – ????????/ ???????? is the rate of decrease of intensity with thickness dx , a is called the absorption co-efficient.
Integration of equation (2) after rearrangement gives,
– ln I = ax+C — — — — — — (3)
Where C is a constant of integration. At x=0, I=Io. So, C = – ln Io. Introducing this in equation (3) we get,
ln I/ Io = – ax — — — — — — (4)
Equation (4) can also be written as,
I = Io ????−???????? — — — — — — (5)
Equation (5) can also be written as,
log I/ Io = − a/ 2.303 x — — — — — (6)
or, log I/ Io = -a` x — — — — — (7)
Where a` (= a /2.303 ) is called extinction co-efficient and -ln I/ Io is termed absorbance of the medium. Absorbance is represented by A.
Lambert’s law was extended by Beer who showed that
when light passes through a solution of a given thickness the fraction of incident light absorbed is dependent not only on the intensity I of light but also on the concentration c of the solution.
This is known as the Beer’s law.
– ???????? /???????? ∝ ???? — — — — — — (8)
The two laws may be combined to write
– ???????? /???????? ∝ ???? × ????
Or, – ???????? /???????? = ???? × ???? × ???? — — — — — (9)
When the concentration, c, is expressed in mol /L, b is called the molar absorption co-efficient.
As in the case of Lambert’s law equation (9) may be transformed into,
log I/ Io = − ???? /2.303 × ???? × ???? — — — — — (10)
log I/ Io = – ∈× ???? × ???? — — — — — (11)
Where ∈ (= ???? / 2.303) is called the molar extinction co-efficient which is expressed in L/mol/cm.
The molar extinction co-efficient ∈ is dependent on the nature of the absorbing solute as well as on the wave length of the incident light used. The expression (equation 11) is commonly known as Beer-Lambert’s law.
Limitations of Beer-Lambert law
The linearity of the Beer-Lambert law is limited by chemical and instrumental factors.
Causes of non-linearity of the law occur in the following conditions:
- deviations in absorptivity coefficients at high concentrations (>0.01M) due to electrostatic interactions between molecules in close proximity
- scattering of light due to particulates in the sample
- fluoresecence or phosphorescence of the sample
- changes in refractive index at high analyte concentration
- shifts in chemical equilibria as a function of concentration
- non-monochromatic radiation, deviations can be minimized by using a relatively flat part of the absorption spectrum such as the maximum of an absorption band
- stray light
Other limitations include:
- The electromagnetic radiation should be monochromatic.
- The light beam should not be scattered.
- The solution should be diluted.
References
- http://life.nthu.edu.tw/~labcjw/BioPhyChem/Spectroscopy/beerslaw.htm
- https://www.slideshare.net/MorshedulHaque/beer-lamberts-law
- https://www.slideshare.net/JALEEL/beer-lambert
- https://en.wikipedia.org/wiki/Beer%E2%80%93Lambert_law
- https://pubs.acs.org/doi/pdf/10.1021/ed074p744.3
- http://www.collin.edu/chemistry/Handouts%202009/Beer’s%20Law.pdf
